
 |
Wissenschaftlicher Werdegang
|
| 1997, 1998, 1999 | Gastforscher, University of Salamanca (jeweils 3 Wochen) |
| 1999 | Gastforscher, Mc Gill University Montreal |
| 1969, 1971, 1982 | Gastforscher, UNAM (Mexiko) und CIMAT (Guanujato, Mexiko) |
Projekt 1:
| Geometrie von Modulräumen holomorpher Vektorbündel und algebraischer Kurven |
1.1 Vektorbündel
Beteiligte Wissenschaftler: Dr. A. Matuschke, Dipl.-Math. Olaf Teschke, David Ploog, Dipl.-Math. Lorenz Wotzlaw, Dr. Georg Hein
Gemeinsam mit Andreas Matuschke wurden Modulräume von Vektorbündeln
über Aufblasungen von Regelflächen untersucht und deren Zusammenhang
mit Instantonen auf ![]() -fach
zusammenhängenden Summen projektiver Ebenen. Zunächst werden
die Ergebnisse beschrieben, die diesen Zusammenhang herstellen. Sei
-fach
zusammenhängenden Summen projektiver Ebenen. Zunächst werden
die Ergebnisse beschrieben, die diesen Zusammenhang herstellen. Sei ![]() eine zu einer
eine zu einer ![]() -fach
zusammenhängenden Summe von projektiven Ebenen diffeomorph
-fach
zusammenhängenden Summe von projektiven Ebenen diffeomorph ![]() -Mannigfaltigkeit.
Ein Modell von
-Mannigfaltigkeit.
Ein Modell von ![]() erhält man wie folgt: Man wähle in
erhält man wie folgt: Man wähle in ![]() eine Gerade
eine Gerade ![]() und
und ![]() Punkte in
Punkte in ![]() ,
blase in diesen Punkten auf, dann erhält man
,
blase in diesen Punkten auf, dann erhält man ![]() und kontrahiere
und kontrahiere ![]() zu einem Punkt
zu einem Punkt ![]() (letzteres läßt sich nicht in der komplex-analytischen Kategorie
ausführen), das Resultat ist diffeomorph zu
(letzteres läßt sich nicht in der komplex-analytischen Kategorie
ausführen), das Resultat ist diffeomorph zu ![]() (ein Minuszeichen heißt: Änderung der Orientierung). Ein Instantonbündel
auf
(ein Minuszeichen heißt: Änderung der Orientierung). Ein Instantonbündel
auf ![]() liefert daher auf
liefert daher auf ![]() ein Vektorbündel
ein Vektorbündel ![]() ,
das längs der Geraden
,
das längs der Geraden ![]() trivial ist, und der selbst-duale Zusammenhang induziert auf
trivial ist, und der selbst-duale Zusammenhang induziert auf ![]() eine holomorphe Struktur. Durch Aufblasung eines Punktes auf
eine holomorphe Struktur. Durch Aufblasung eines Punktes auf ![]() erhält man eine Fläche
erhält man eine Fläche ![]() mit einer Faserung
mit einer Faserung ![]() ,
die aus einer Regelfläche mit einem ausgezeichneten Schnitt
,
die aus einer Regelfläche mit einem ausgezeichneten Schnitt ![]() (die exzeptionelle Kurve von
(die exzeptionelle Kurve von ![]() )
durch Aufblasung in
)
durch Aufblasung in ![]() Punkten aus
Punkten aus ![]() in
in ![]() verschiedenen Fasern entsteht. Sei
verschiedenen Fasern entsteht. Sei ![]() das zurückgezogene Bündel
das zurückgezogene Bündel ![]() auf
auf ![]() .
Die Wahl einer Basis des Instantonbündels im Punkte
.
Die Wahl einer Basis des Instantonbündels im Punkte ![]() ist äquivalent zur Wahl einer Trivialisierung von
ist äquivalent zur Wahl einer Trivialisierung von ![]() bzw. zur Wahl einer Trivialisierung von
bzw. zur Wahl einer Trivialisierung von ![]() .
Auf diese Weise erhält man eine Korrespondenz zwischen Isomorphieklassen
markierter
.
Auf diese Weise erhält man eine Korrespondenz zwischen Isomorphieklassen
markierter ![]() -Instantonen
auf
-Instantonen
auf ![]() (Markierung heißt: Wahl einer Basis in
(Markierung heißt: Wahl einer Basis in ![]() )
und Isomorphieklassen gerahmter
)
und Isomorphieklassen gerahmter ![]() -Bündel
auf
-Bündel
auf ![]() (Rahmung heißt: Wahl einer Trivialisierung auf
(Rahmung heißt: Wahl einer Trivialisierung auf ![]() ),
die auf der Faser
),
die auf der Faser ![]() trivial sind. Mit Hilfe der Penrose-Ward-Korrespondenz wurde (für
die konstruierten selbst-dualen Strukturen auf
trivial sind. Mit Hilfe der Penrose-Ward-Korrespondenz wurde (für
die konstruierten selbst-dualen Strukturen auf ![]() )
gezeigt in [6]. Satz. Ist
)
gezeigt in [6]. Satz. Ist ![]() der Modulraum der markierten
der Modulraum der markierten ![]() -Instantonen
auf
-Instantonen
auf ![]() mit Quantenzahl
mit Quantenzahl ![]() ,
und ist
,
und ist ![]() der Modulraum der gerahmten
der Modulraum der gerahmten ![]() -Bündel
-Bündel ![]() auf
auf ![]() mit
mit ![]() ,
die auf der Faser
,
die auf der Faser ![]() trivial sind, so ist die oben beschriebene Korrespondenz ein reell-analytischer
Isomorphismus
trivial sind, so ist die oben beschriebene Korrespondenz ein reell-analytischer
Isomorphismus
Dieses Resultat legt also folgende Fragen nahe: Es sei ![]() eine Faserung einer Fläche über einer glatten Kurve
eine Faserung einer Fläche über einer glatten Kurve ![]() ,
die aus einer Regelfläche
,
die aus einer Regelfläche ![]() mit einem Schnitt
mit einem Schnitt ![]() durch Aufblasung von
durch Aufblasung von ![]() verschiedenen Punkten aus
verschiedenen Punkten aus ![]() entsteht. Dann konstruiere man einen Modulraum
entsteht. Dann konstruiere man einen Modulraum ![]() von
von ![]() -Bündeln
-Bündeln ![]() mit
mit ![]() ,
mit einer Rahmung
,
mit einer Rahmung ![]() ,
die auf einer Faser trivial sind, und beschreibe dessen Struktur. Die Existenz
eines solchen Modulraumes läßt sich auf ein Existenzkriterium
von Huybrechts-Lehn zurückführen, wo folgende Bedingungen als
hinreichend für die Existenz eines feinen Modulraumes nachgewiesen
werden.
,
die auf einer Faser trivial sind, und beschreibe dessen Struktur. Die Existenz
eines solchen Modulraumes läßt sich auf ein Existenzkriterium
von Huybrechts-Lehn zurückführen, wo folgende Bedingungen als
hinreichend für die Existenz eines feinen Modulraumes nachgewiesen
werden.
so bilden diese eine offene Überdeckung und ![]() ist ampel für
ist ampel für ![]() .
Die Rahmung
.
Die Rahmung ![]() induziert eine eindeutig bestimmte Rahmung von
induziert eine eindeutig bestimmte Rahmung von ![]() auf
auf ![]() .
Daher sind diese Funktoren
.
Daher sind diese Funktoren ![]() darstellbar und damit auch
darstellbar und damit auch ![]() .
Standartresultate der Deformationstheorie ergeben, daß
.
Standartresultate der Deformationstheorie ergeben, daß ![]() glatt von der (komplexen) Dimension
glatt von der (komplexen) Dimension ![]() .
Weitere Strukturaussagen über diese Modulräume sind in [6] erzielt
worden. Hier einige Resultate: (1) Es gibt einen surjektiven Morphismus
mit zusammenhängenden Fasern
.
Weitere Strukturaussagen über diese Modulräume sind in [6] erzielt
worden. Hier einige Resultate: (1) Es gibt einen surjektiven Morphismus
mit zusammenhängenden Fasern
Ist 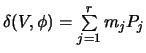 ,
so sind die Fasern über
,
so sind die Fasern über ![]() genau die Sprungfasern, und
genau die Sprungfasern, und ![]() ist ein Vektorraum der Dimension
ist ein Vektorraum der Dimension ![]() .
Hieraus folgt insbesondere, daß
.
Hieraus folgt insbesondere, daß ![]() nicht-leer und zusammenhängend ist. (2) Die Fasern über
nicht-leer und zusammenhängend ist. (2) Die Fasern über 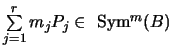 sind reduziert und von der Form
sind reduziert und von der Form ![]() und
und
[4] ![]() hängt nur vom
hängt nur vom ![]() und dem Fasertyp ab. (3) Für die
und dem Fasertyp ab. (3) Für die ![]() werden verschiedene Beschreibungen angegeben. Insbesondere: Der glatte
Ort
werden verschiedene Beschreibungen angegeben. Insbesondere: Der glatte
Ort ![]() von
von ![]() besteht genau aus den Bündeln (auf dem Keim der Faser
besteht genau aus den Bündeln (auf dem Keim der Faser ![]() )
mit
)
mit ![]() .
Wenn
.
Wenn ![]()
![]() Komponenten hat, so hat
Komponenten hat, so hat ![]() Zusammenhangskomponenten, die alle isomorph zu einem homogenen Raum
Zusammenhangskomponenten, die alle isomorph zu einem homogenen Raum ![]() sind.
sind. ![]() sind die Gruppen
sind die Gruppen
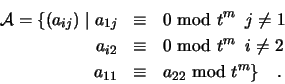
wobei ![]() folgende Invariante ist: Die Familie sei in allgemeinen Punkten
folgende Invariante ist: Die Familie sei in allgemeinen Punkten ![]() vollständig, dann ist
vollständig, dann ist ![]() ,
wobei
,
wobei ![]() Kern der Surjektion
Kern der Surjektion
(![]() das Normalenbündel der Kurve
das Normalenbündel der Kurve ![]() in
in ![]() ).
Beispiele:
(1) Für die Familie der Geraden auf einer Quadrik
).
Beispiele:
(1) Für die Familie der Geraden auf einer Quadrik ![]() ,
ebenso für die Familie der Twistorgeraden auf einem Twistorraum ist
,
ebenso für die Familie der Twistorgeraden auf einem Twistorraum ist ![]() . (2) Wenn
. (2) Wenn ![]()
![]() -dimensional
und eine Spin-Struktur besitzt, d.h.
-dimensional
und eine Spin-Struktur besitzt, d.h. ![]() und wenn das Linearsystem
und wenn das Linearsystem ![]() frei von der Dimension
frei von der Dimension ![]() ist und
ist und ![]() ,
so gilt für die Familie der vollständigen Durchschnitte von zwei
Flächen aus
,
so gilt für die Familie der vollständigen Durchschnitte von zwei
Flächen aus ![]()
In diesem Fall läßt sich für Bündel ![]() vom Rang
vom Rang ![]() die Kohomologie
die Kohomologie ![]() bzw.
bzw. ![]() mittels des Spektrums in Analogie zu Bündeln auf
mittels des Spektrums in Analogie zu Bündeln auf ![]() studieren (wobei
studieren (wobei ![]() an die Stelle von
an die Stelle von ![]() tritt,
tritt, ![]() ist aber im allgemeinen nicht ampel). Wir hoffen, daß diese Untersuchungen
Anwendungen beim Studium mathematischer Instantonbündel auf allgemeineren
Twistorräumen finden können.
ist aber im allgemeinen nicht ampel). Wir hoffen, daß diese Untersuchungen
Anwendungen beim Studium mathematischer Instantonbündel auf allgemeineren
Twistorräumen finden können.
1.2. Modulräume von Kurven
Ziel ist der Ausbau der Krichever-Korrespondenz. Diesbezügliche
Untersuchungen wurden von der Doktorandin I. Quandt geführt ([10],
[11]). Es geht darum, diese Korrespondenz zwischen kommutativen Ringen
von (formalen) gewöhnlichen Differential-Operatoren einer Veränderlichen
und gewissen geometrischen Daten (einer projektiven algebraischen Kurve
mit einem ausgezeichneten glatten Punkt, sowie einer torsionsfreien kohährenten
Garbe auf der Kurve, so daß in dem Punkt ein ausgezeichneter formaler
lokaler Parameter und eine ausgezeichnete Trivialisierung gegenben sind)
auf den Fall von Familien von solchen Daten, über einer geeigneten
Klasse von Basisschemata ![]() auszudehnen. Eigentlich sollten auch höher-dimensionale Analoga dieser
Korresponendenz gefunden werden, Frau Quandt ist aber inzwischen ausgeschieden,
so daß die Untersuchungen in dieser Richtung zunächst nicht
weitergeführt wurden. Die geometrischen Daten sind zu interpretieren
als Spektraldaten des Ringes von Differential-Operatoen, da die Betrachtung
rein lokal ist (keine Randbedingungen) ist das Spektrum sehr groß
und entspricht den Punkten der Kurve, die Garbe
auszudehnen. Eigentlich sollten auch höher-dimensionale Analoga dieser
Korresponendenz gefunden werden, Frau Quandt ist aber inzwischen ausgeschieden,
so daß die Untersuchungen in dieser Richtung zunächst nicht
weitergeführt wurden. Die geometrischen Daten sind zu interpretieren
als Spektraldaten des Ringes von Differential-Operatoen, da die Betrachtung
rein lokal ist (keine Randbedingungen) ist das Spektrum sehr groß
und entspricht den Punkten der Kurve, die Garbe ![]() besteht aus den Eigenfunktionen. Ein Analogon der Krichever-Korrespondenz
wurde für den Fall beliebiger affiner Basisschemata gefunden und in
enger Zusammenarbeit mit M. Mulase ausgearbeitet [10], [11]. Weiterhin
liegen einige Untersuchungen von H. Kurke vor über unendliche Grassmannsche,
die aber wegen des Ausscheidens von Frau Quandt z.Zt. ebenfalls ruhen.
Das Thema soll allerdings in nächster Zeit weitergeführt werden.
besteht aus den Eigenfunktionen. Ein Analogon der Krichever-Korrespondenz
wurde für den Fall beliebiger affiner Basisschemata gefunden und in
enger Zusammenarbeit mit M. Mulase ausgearbeitet [10], [11]. Weiterhin
liegen einige Untersuchungen von H. Kurke vor über unendliche Grassmannsche,
die aber wegen des Ausscheidens von Frau Quandt z.Zt. ebenfalls ruhen.
Das Thema soll allerdings in nächster Zeit weitergeführt werden.
Projekt 2:
| Selbstduale Strukturen |
Beteiligte Wissenschaftler: Dr. Ingo Hadan, Dipl. Math. Achim Radtke
In der Dissertation von I. Hadan und den Arbeiten [17], [9] wurden Untersuchungen
durchgeführt, die zum Ziel eine Beschreibung des Modulraumes aller
selbst-dualen konformen Strukturen auf ![]() hat. Allerdings erweist sich dies schwieriger als vermutet. Die Situation
stellt sich wie folgt dar: Aus den Arbeiten von H. Kurke und B. Kreussler
- H. Kurke aus der früheren Berichtsperiode ist bekannt, daß
eine einfach zusammenhängende
hat. Allerdings erweist sich dies schwieriger als vermutet. Die Situation
stellt sich wie folgt dar: Aus den Arbeiten von H. Kurke und B. Kreussler
- H. Kurke aus der früheren Berichtsperiode ist bekannt, daß
eine einfach zusammenhängende ![]() -Mannigfaltigkeit
-Mannigfaltigkeit ![]() mit der Schnittform
mit der Schnittform ![]() diffeomorph zu
diffeomorph zu ![]() ist, sofern sie eine selbst-duale konforme Struktur besitzt, und daß
als Twistorraum nur in Frage kommt, die Modifikation einer Doppelüberlagerung
von
ist, sofern sie eine selbst-duale konforme Struktur besitzt, und daß
als Twistorraum nur in Frage kommt, die Modifikation einer Doppelüberlagerung
von ![]() verzweigt längs einer Fläche
verzweigt längs einer Fläche ![]() -ten
Grades mit genau
-ten
Grades mit genau ![]() Doppelpunkten, oder Modifikationen von bestimmten Kegelschnittbündeln
über einer Quadrik. Der Fall von Doppelüberlagerungen wurde eingehend
von B. Kreussler untersucht im Hinblick auf die Frage, welche eine Twistorraumstruktur
besitzen, ohne daß tatsächlich eine gefunden wurde. Andererseits
wurden von H. Kurke Familien von Kegelschnittbündeln über einer
Quadrik gefunden, die nach einer bestimmten Modifikation eine Twistorraum-Struktur
besitzen, und zwar für jedes
Doppelpunkten, oder Modifikationen von bestimmten Kegelschnittbündeln
über einer Quadrik. Der Fall von Doppelüberlagerungen wurde eingehend
von B. Kreussler untersucht im Hinblick auf die Frage, welche eine Twistorraumstruktur
besitzen, ohne daß tatsächlich eine gefunden wurde. Andererseits
wurden von H. Kurke Familien von Kegelschnittbündeln über einer
Quadrik gefunden, die nach einer bestimmten Modifikation eine Twistorraum-Struktur
besitzen, und zwar für jedes ![]() eine Familie, die durch eine Konfiguration von
eine Familie, die durch eine Konfiguration von ![]() verschiedenen Punkten im hyperbolischen Raum, modulo Isometrien, parametrisiert
wird, und die zu selbst-dualen konformen Strukturen auf der
verschiedenen Punkten im hyperbolischen Raum, modulo Isometrien, parametrisiert
wird, und die zu selbst-dualen konformen Strukturen auf der ![]() -fachen
zusammenhängenden Summe projektiver Ebenen gehört. Diese selbst-dualen
Strukturen wurden unabhängig von C. Le Brun gefunden. Für
-fachen
zusammenhängenden Summe projektiver Ebenen gehört. Diese selbst-dualen
Strukturen wurden unabhängig von C. Le Brun gefunden. Für ![]() erhält man eine dreidimensionale Familie, während die Deformationstheorie
ergibt, daß die universelle Deformation Sechsdimensional ist. Somit
kann man indirekt darauf schließen, daß gewisse Doppelüberlagerungen
eine Twistorraumstruktur besitzen. Als äußerst schwierig erweist
es sich, die Twistorgeraden zu identifizieren. Die allgemeinen Twistorgeraden
müssen Kurven auf der Doppelüberlagerung sein, deren Projektion
in
erhält man eine dreidimensionale Familie, während die Deformationstheorie
ergibt, daß die universelle Deformation Sechsdimensional ist. Somit
kann man indirekt darauf schließen, daß gewisse Doppelüberlagerungen
eine Twistorraumstruktur besitzen. Als äußerst schwierig erweist
es sich, die Twistorgeraden zu identifizieren. Die allgemeinen Twistorgeraden
müssen Kurven auf der Doppelüberlagerung sein, deren Projektion
in ![]() Kegelschnitte sein müssen, die die Verzweigungsfläche
Kegelschnitte sein müssen, die die Verzweigungsfläche ![]() in alle Schnittpunkten von gerader Ordnung berühren. Die Arbeit von
I. Hadan untersucht ausführlich und systematisch das Hilbertschema
dieser Kurven für Doppelüberlagerungen mit beliebiger Verzweigungsfläche
vom Grad
in alle Schnittpunkten von gerader Ordnung berühren. Die Arbeit von
I. Hadan untersucht ausführlich und systematisch das Hilbertschema
dieser Kurven für Doppelüberlagerungen mit beliebiger Verzweigungsfläche
vom Grad ![]() ,
vorausgesetzt diese hat höchstens gewöhnliche Doppelpunkte. Sie
ist unabhängig vom Ausgangsproblem von selbständigem Interesse.
Als Fazit kann man ziehen, daß das Hilbertschema dieser Kurven sehr
viele irreduzible Komponenten haben kann und diese Anzahl abhängen
kann von der Anzahl der Doppelpunkte und der Anzahl und Existenz von Tope-Ebenen.
Zum Beispiel können
,
vorausgesetzt diese hat höchstens gewöhnliche Doppelpunkte. Sie
ist unabhängig vom Ausgangsproblem von selbständigem Interesse.
Als Fazit kann man ziehen, daß das Hilbertschema dieser Kurven sehr
viele irreduzible Komponenten haben kann und diese Anzahl abhängen
kann von der Anzahl der Doppelpunkte und der Anzahl und Existenz von Tope-Ebenen.
Zum Beispiel können ![]() irreduzible Komponenten auftreten, das ist der Fall, wenn die Quartik
irreduzible Komponenten auftreten, das ist der Fall, wenn die Quartik ![]()
![]() Doppelpunkte und
Doppelpunkte und ![]() Trope-Ebenen hat. In dem für Twistorräume interessierenden Fall
hat die Quartik
Trope-Ebenen hat. In dem für Twistorräume interessierenden Fall
hat die Quartik ![]() Doppelpunkte und
Doppelpunkte und ![]() Trope-Ebenen, in diesem Fall hat man
Trope-Ebenen, in diesem Fall hat man ![]() Komponenten, von denen
Komponenten, von denen ![]() Kandidaten für Twistorfaserungen sind. Dies zeigt die Schwierigkeit,
die möglichen Twistorfaserungen genau zu finden, eine weitere Schwierigkeit
besteht darin, daß man in
Kandidaten für Twistorfaserungen sind. Dies zeigt die Schwierigkeit,
die möglichen Twistorfaserungen genau zu finden, eine weitere Schwierigkeit
besteht darin, daß man in ![]() Punkten eine Wahl zu treffen hat für eine kleine Auflösung. Unabhängig
von diesem Problem stellen die Untersuchungen einen wichtigen Beitrag zur
Geometrie von Doppelsolids dar und es wird ein interessanter Beitrag zum
Studium von Monodromiewirkungen geleistet. Gemeinsam mit A. Radtke wurden
sogenannte
Punkten eine Wahl zu treffen hat für eine kleine Auflösung. Unabhängig
von diesem Problem stellen die Untersuchungen einen wichtigen Beitrag zur
Geometrie von Doppelsolids dar und es wird ein interessanter Beitrag zum
Studium von Monodromiewirkungen geleistet. Gemeinsam mit A. Radtke wurden
sogenannte ![]() -Strukturen
auf komplexen Mannigfaltigkeiten untersucht. Dies stellt eine Verallgemeinerung
von Twistorräumen dar. Die in Vorbereitung befindliche Dissertation
von A. Radtke gibt eine teilweise Klassifizierung von
-Strukturen
auf komplexen Mannigfaltigkeiten untersucht. Dies stellt eine Verallgemeinerung
von Twistorräumen dar. Die in Vorbereitung befindliche Dissertation
von A. Radtke gibt eine teilweise Klassifizierung von ![]() -Mannigfaltigkeiten
mit
-Mannigfaltigkeiten
mit ![]() -Strukturen
dar, verallgemeinert und systematisiert frühere Arbeiten der japanischen
Schule.
-Strukturen
dar, verallgemeinert und systematisiert frühere Arbeiten der japanischen
Schule.
Drittmittel: Die DFG hat dieses Projekt im Rahmen des Schwerpunktes
,,Komplexe Mannigfaltigkeiten`` bzw. des Projektes (Nr. Ku 770/1-3) gefördert;
weiterhin durch das TMR-Projekt AGE (,,Algebraic Geometry in Europa``),
Knoten Hannover, Essen, Hamburg, Berlin.
Publikationen
Preprints