Prof. Dr. Jürgen Leiterer

 

Wissenschaftlicher Werdegang

1964-1968	Studium der Mathematik in Jena und Berlin
1968	Diplom an der Universität Jena
1968-1972	weiteres Studium und Forschungsarbeit bei I. Gohberg in Kischinjow
1971	Promotion (Dr. rer. nat.)
1972-1974	Oberassistent in Jena
1974	Promotion B an der Universität Jena
1974-1989	wissenschaftlicher Mitarbeiter am Institut für Mathematik der Akademie der Wissenschaften der DDR in Berlin
1983	Ernennung zum Akademie-Professor
1989	Professor an der Humboldt-Universität zu Berlin
seit 1993	Professor (C4) für Mathematik/Komplexe Analysis an der Humboldt-Universität zu Berlin

Projekt: Mehrdimensionale Cauchy-Riemann-Gleichung und Vektorbündel
 

Kooperationspartner: C. Laurent (Grenoble) und G. Henkin (Paris VI)

Bei der Cauchy-Riemann-Gleichung geht es besonders um die Konstruktion von Lösungs- bzw. Homotopieoperatoren mit gleichmäßigen Abschätzungen. Solche Abschätzungen lassen Aussagen über das Randverhalten der Cauchy-Riemann-Gleichung zu. Auf diese Weise kann man die Einschränkung der Cauchy-Riemann-Gleichung auf Ränder und, allgemeiner, auf reelle Untermannigfaltigkeiten mit konstanter komplexer Tangentialdimension untersuchen. Solche reellen Mannigfaltigkeiten heißen Cauchy-Riemann-Mannigfaltigkeiten und die Einschränkung der Cauchy-Riemann-Gleichung darauf bezeichnet man als die tangentiale Cauchy-Riemann-Gleichung. Bei den Vektorbündeln geht es um Existenz und Eindeutigkeit von holomorphen (bzw. Cauchy-Riemann-) Strukturen. Dies führt auf nichtlineare Gleichungen, deren linearer Teil die Cauchy-Riemann-Gleichung (bzw. die tangentiale Cauchy-Riemann-Gleichung) ist. Hat man Homotopieoperatoren mit hinreichend guten gleichmäßigen Abschätzungen für diesen linearen Teil, so führt das unter Umständen zur lokalen Lösung des nichtlinearen Problems. Im Anschluß daran geht es um das Zusammenfügen dieser lokalen Lösungen zu einer globalen Lösung. Besonders interessant ist dann die Frage, inwieweit einer globalen Lösung noch komplex-analytische Hindernisse entgegenstehen oder ob man ein sogenanntes Okasches Prinzip hat, d.h. alles bereits durch die Topologie bestimmt ist.

Publikationen

[1]

Laurent-Thiébaut, C.; Leiterer, J.: The Andreotti-Vesentini separation theorem and global homotopy representation. Math. Zeitschrift 227 (1998), 711-727.

[2]

Henkin, G.; Leiterer, J.: The Oka-Grauert Principle without induction over the base dimension. Math. Ann. 311 (1998), 71-93.

[3]

Merker, J.; Porten, E.: On the local meromorphic extension of CR-meromorphic mappings. Ann. Pol. math. 70 (1998), 163-193.

[4]

Merker, J.; Porten, E.: Enveloppe d'holomorphic locale des variétés CR et éliminations des singularités pour les fonctions CR integrables. C.R. Acad. Sci. Paris, Ser. I, 1999.

[5]

Laurent-Thiébaut, C.; Leiterer, J.: Some applications of Serre duality in 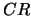$CR$-manifolds. Nagoya Math. Journal 154 (1999), 141-156.

[6]

Laurent-Thiébaut, C.; Leiterer, J.: Isomorphisme de Dolbeault dans les variétés 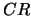$CR$. C.R. Acad. Sci. Paris, Ser. I, 1999, 469-472.

[7]

Laurent-Thiébaut, C.; Leiterer, J.: On Serre duality. Bulletin des Sciences Matheématiques 124 (2000) 2, 93-106.

[8]

Laurent-Thiébaut, C.; Leiterer, J.: Malgrange's vanishing theorem in 1-concave 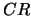$CR$ manifolds. Nagoya Math. Journal 157 (2000).

[9]

Laurent-Thiébaut, C.; Leiterer, J.: The Malgrange vanishing theorem with support conditions. In: Proceedings du Congrès en l'honneur de Pierre Lelong. Paris, septembre 97, Progress in Math., Birkhäuser, 2000.

[10]

Laurent-Thiébaut, C.; Leiterer, J.: An Andreotti-Vesentini separation theorem on real hypersurfaces. Annali di Matematica pura et Applicata.

[11]

Merker, J.; Porten, E.: On removable singularities for integrable CR functions. Erscheint in: Indiana Univ. Math. J..

[12]

Merker, J.; Porten, E.: Metrically thin singularities of integrable CR functions. Erscheint in: Intern. J. Math..