
 |
Wissenschaftlicher Werdegang
|
| seit 1992 | wissenschaftlicher Mitarbeiter des Instituts für Angewandte Analysis und Stochastik im Forschungsverbund Berlin e.V. (jetzt Weierstraß-Institut für Angewandte Analysis und Stochastik) |
| seit 1993 | Professor (C4) für Mathematik/Angewandte Analysis an der Humboldt-Universität zu Berlin |
Projekt 1:
| Regularitätsaussagen für Lösungen von Randwertproblemen und Rand-Anfangswertproblemen bei nichtglatten Daten |
Beteiligte Wissenschaftler: Dr. sc. L. Recke (Humboldt-Universität), Dipl-Math. J. A. Griepentrog (Weierstraß-Institut für Angewandte Analysis und Stochastik)
Kooperationspartner: Prof. Dr. O. John, Prof. Dr. J. Stara (beide Karls-Universität Prag)
Die Modellierung des Ladungsträgertransports in Halbleiterbauelementen
führt auf Randwertprobleme und Rand-Anfangswertprobleme mit sich sprunghaft
ändernden Koeffizienten und Randbedingungen. Diese Probleme sind bisher
im Rahmen der Skalen der Sobolev-Räume ![]() und
und ![]() untersucht worden. Die für die Rand-Anfangswertprobleme erreichten
Ergebnisse sind nur im räumlich zweidimensionalen Fall als befriedigend
anzusehen. Es besteht deshalb weiterhin Bedarf an Regularitätsergebnissen
für Probleme mit nichtglatten Daten.
untersucht worden. Die für die Rand-Anfangswertprobleme erreichten
Ergebnisse sind nur im räumlich zweidimensionalen Fall als befriedigend
anzusehen. Es besteht deshalb weiterhin Bedarf an Regularitätsergebnissen
für Probleme mit nichtglatten Daten.
Als Alternative für die Räume ![]() bieten sich gewisse Sobolev-Campantato-Räume an. Zu diesen Räumen
passende Analoga der Räume
bieten sich gewisse Sobolev-Campantato-Räume an. Zu diesen Räumen
passende Analoga der Räume ![]() (,,Sobolev-Campanato-Räume von Funktionalen``) sind jedoch bisher
nicht etabliert und kaum untersucht. Dem versucht die Arbeit [2] abzuhelfen.
Hauptergebnis der Arbeit ist die Feststellung, dass zu allen Sobolev-Campanato-Räumen
präduale Banachräume existieren. Die benutzte Methode, die Konstruktion
neuer Banachräume als einer Art von projektiven und induktiven Limites,
ist auch im Zusammenhang mit anderen Räumen von Funktionen bzw. Funktionalen
von Interesse.
(,,Sobolev-Campanato-Räume von Funktionalen``) sind jedoch bisher
nicht etabliert und kaum untersucht. Dem versucht die Arbeit [2] abzuhelfen.
Hauptergebnis der Arbeit ist die Feststellung, dass zu allen Sobolev-Campanato-Räumen
präduale Banachräume existieren. Die benutzte Methode, die Konstruktion
neuer Banachräume als einer Art von projektiven und induktiven Limites,
ist auch im Zusammenhang mit anderen Räumen von Funktionen bzw. Funktionalen
von Interesse.
Dass die erwähnten Sobolev-Campanato-Räume von Funktionalen
ein natürliches Hilfsmittel für die Untersuchung der Regularität
von Lösungen von linearen Randwertproblemen und Rand-Anfangswertproblemen
sind, wird in der Dissertation von Jens A. Griepentrog [1] gezeigt.
Projekt 2:
| Mathematische Modellierung von Chemotaxisvorgängen |
Beteiligte Wissenschaftler: Dipl.-Math. (jetzt Dr.) K. Post (Humboldt-Universität)
Kooperationspartner: Prof. Dr. H. Gajewski, Dr. K. Zacharias (beide Weierstraß-Institut für Angewandte Analysis und Stochastik), Prof. Dr. B. Kawohl (Universität Köln)
Unter Chemotaxis versteht man das Phänomen, daß bestimmte
Organismen auf den Gradienten einer chemischen Substanz durch eine Bewegung
in Richtung dieses Gradienten reagieren. Häufig wird dabei die Substanz
von den Organismen selbst erzeugt.
Die mathematische Modellierung von Chemotaxisvorgängen führt
auf Gleichungen der Form
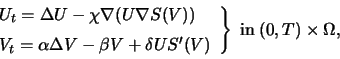 |
(1) |
Publikationen