| non-mobile-version | mobile-version |
Higgs Bundles, K3 Surfaces and Moduli
A Conference of the Kolleg Mathematik Physik Berlin (KMPB, an Interdisciplinary Research Center for Mathematics and Physics)
Humboldt Universität zu Berlin
10 - 12 July 2017
Speakers
Piotr Achinger (IHES)
François Charles (Paris Orsay)
Michael Gröchenig (Berlin)
Tamás Hausel (IST Austria)
Jochen Heinloth (Essen)
Sean Keel (Austin)
Michael Kemeny (Stanford)
Alexander Kuznetsov (Moscow)
Christian Liedtke (Munich)
Keiji Oguiso (Tokyo)
Matthias Schütt (Hanover)
Organizers
Registration
The registration is closed.
Participants
full list of participants (last update: Thu, 13.07.2017 08:05:34)
Programme
Abstracts
Piotr Achinger
Log geometry, monodromy, and Betti realization of varieties
defined by formal power series
A now classical construction due to Kato and Nakayama attaches a topological space ("Betti realization") to a log scheme over C. I will show how this construction can be used to recover the topological germ of a log smooth degeneration from the log special fiber alone. In particular, I will show how to compute the monodromy of the family directly from the log special fiber. In a different direction, I will also explain how Kato–Nakayama spaces can be employed to functorially attach homotopy types to varieties defined over the field C((t)) of formal Laurent series. For varieties defined by convergent series, this construction agrees with the usual one, obtained via complex topology. The first half is joint work with Arthur Ogus, the second is joint with Mattia Talpo. Almost no prior exposure to log geometry will be required.François Charles
Some remarks on boundedness results for K3 surfaces
There are many conjectured finiteness results for invariants of K3 surfaces defined over number fields. After discussing some of these conjectures and known results, we will discuss uniform boundedness for the Brauer groups of surfaces over number fields in one-parameter families. This is joint work with Anna Cadoret. Michael Gröchenig
p-adic integration for the Hitchin system
I will report on joint work with D. Wyss and P. Ziegler. We prove a conjecture by Hausel-Thaddeus which predicts an agreement of appropriately defined Hodge numbers for moduli spaces of Higgs bundles for the structure groups SL(n) and PGL(n) over the complex numbers. Despite the complex-analytic nature of the statement our proof is entirely arithmetic.Tamás Hausel
Mirror symmetry with branes by equivariant Verlinde formulae
I will discuss an agreement of equivariant indices of semi-classical homomorphisms between pairwise mirror branes in the GL2 Higgs moduli space on a Riemann surface. One side we have the components of the Lagrangian brane of U(1,1) Higgs bundles whose mirror was proposed by Nigel Hitchin to be certain even exterior powers of the hyperholomorphic Dirac bundle on the SL2 Higgs moduli space. The agreement arises from a mysterious Hard Lefschetz type functional equation. This gives strong computational evidence for Hitchin’s proposal. This is joint work with Anton Mellit and Du Pei.Jochen Heinloth
Supports of the cohomology of Hitchin's fibrations
Hitchin's fibrations have a very rich geometry and the singularites of the fibers contain arithmetically interesting information. For generalizations of the original fibration Ngo's support theorem can be used to show that miracously one can often obtain all of this information from the smooth part of the fibration alone.
However, these arguments break down for in the original symplectic moduli space of Higgs bundles, which has a particularly interesting geometry. Quite a few results on the geometry of these moduli spaces have been obtained using smooth fibers alone, but it turns out that in this case although the symplectic imposes restrictions on contributions from singular fibers, it turns out that contributions form the singular fibers do appear.
This is a report on a joint work in progress with M. de Cataldo and L. Migliorini. Sean Keel
The secondary fan for log CYs
I'll explain my (I hope surprising) conjecture that a natural moduli space of Fanos with anti-canonical divisor is a toric variety, generalizing the toric case due to Gelfand-Kapranov-Zelevinski and Alexeev; and ongoing work, joint with Tony Yu and Paul Hacking, mixing Mori theory, mirror symmetry, and rigid analytic geometry, to prove it for del Pezzo surfaces. Michael Kemeny
Degenerations of projective K3 surfaces and paracanonical curves
In a beautiful recent paper, Arbarello, Bruno and Sernesi classify projective degenerations of K3 surfaces for which the hyperplane sections remain reasonably general. Whilst the original application of this classification was to prove Wahl's Conjecture characterizing the locus of curves arising as hyperplane sections of a K3 surface, several new applications have since been found. We will explain how one of the most important cases of the classification, namely the case where the resolution of the degenerate K3 is a scroll over an elliptic curve, can be used to study paracanonical curves, i.e. curves together with an l-torsion point. In particular, this gives a proof of the odd genus case of the Prym-Green conjecture which describes the equations defining such curves in projective space. This is joint work with G. Farkas
Alexander Kuznetsov
Quadric fibrations in the Grothendieck ring of varieties
with an application to Mukai dual K3 surfaces
I will discuss a relation in the Grothendieck ring of varieties associated with a hyperbolic reduction of a quadric fibration. This relation will be applied to show that the differences of classes of a K3 surface of degree 8 and of a K3 surface of degree 2 (associated to it as a certain moduli space of vector bundles) is annihilated by the class of an affine line, as soon as the natural Brauer class on the latter K3 surface vanishes. This is a joint work with Evgeny Shinder.Christian Liedtke
Crystalline Galois Representations arising from K3 Surfaces
Let K be a p-adic field, let X be a K3 surface over K, and assume that X has potential semi-stable reduction. Then, we show that the following are equivalent:
the l-adic Galois representation on H2(X,Ql) is unramified for one l different from p
the l-adic Galois representation on H2(X,Ql) is unramified for all l different from p
the p-adic Galois representation on H2(X,Qp) is crystalline
the surface has good reduction after an unramified extension of K
This is an analog of the classical Serre-Tate theorem for Abelian varieties. We also show by counter-examples that neither 1), nor 2), nor 3) implies that X has good reduction of X over K. However, in this case X admits a proper model over OK, whose special fiber X0 has at worst canonical singularities. Part of this is joint with Matsumoto, part of this is joint with Chiarellotto and Lazda.
Keiji Oguiso
On homeomorphism type of projective fourfolds
It is natural to ask how similar or different algebro-geometric structure of oriented homeomorphic (with respect to Euclidean topology) projective manifolds. This question has a long history since a work of Kodaira-Hirzebruch but not much are known even now in dimension ≥ 3.
In this talk, after reviewing a brief history and why fourfolds (rather than threefolds), I would like to discuss this problem for fourfolds of basic types, say Fano, Calabi Yau and hyperkähler fourfold. In particular, I would like to present:
1) Fano fourfolds are never oriented homeomorphic to manifolds with trivial first Chern class.
2) Coarse classification of fourfolds in terms of numerical Kodaira dimension oriented homomorphic to the Hilbert scheme of two points of K3 surfaces (one of two known hyperkähler fourfolds up to deformation) together with the existence of exiotic algebro-geometric structure.
This is a joint work with Professor Thomas Peternell in Bayreuth.
Matthias Schütt
Enriques surfaces with maximal root types: moduli and good reduction
I will review recent results on Enriques surfaces admitting maximal configurations of smooth rational curves, with emphasis on the characteristic two case. In particular, we will study the moduli of these Enriques surfaces and work out applications to good reduction, both for Enriques and K3 surfaces.
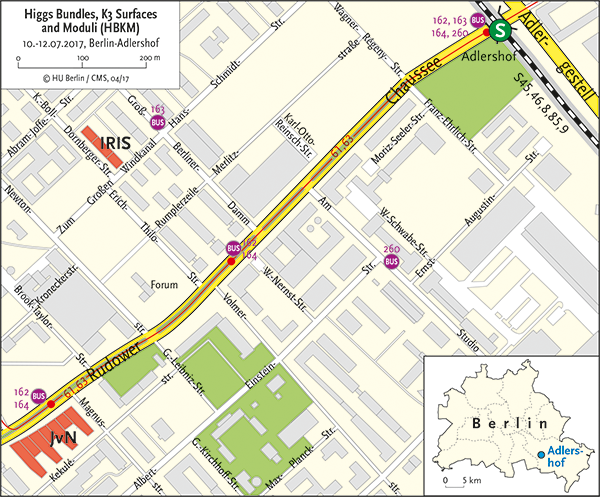
Venue
All lectures will take place in the IRIS Adlershof building of the Humboldt
University at
Zum Großen Windkanal 6
Room: 221
12489 Berlin