Registration
The registration is closed.
Participants
full list of participants
Programme
Abstracts Valery Alexeev — Geometric compactifications of K3 moduli Valery Alexeev — Geometric compactifications of K3 moduli
I will describe, in several special cases, compactifications of moduli spaces of K3 surfaces obtained by adding stable pairs on the boundary. Parts are joint with Alan Thompson. Arnaud Beauville — The Chow ring of hyperkähler manifolds Arnaud Beauville — The Chow ring of hyperkähler manifolds
This is a survey of the progress obtained in the last 10 years on the Chow ring of projective hyperkähler manifolds. Starting from the case of K3 surfaces, I will explain why one may hope that this Chow ring admits a natural grading. While this conjecture seems inaccessible at this moment, it implies some concrete consequences on intersections of divisors, which have been verified in an increasing number of cases. Jérémy Blanc — Structure of the Cremona groups Jérémy Blanc — Structure of the Cremona groups
In this talk I will survey some results on the Cremona groups, which are the groups of birational transformations of projective spaces.
In dimension 2, some new results were appearing recently and give us now a quite good information about the group. Some of them appear to use the action of the Cremona group on a hyperbolic space of infinite dimension. However, this action does not seem to generalise easily in higher dimension.
I will also talk about the possible structures that one can endow the groups with. Fabrizio Catanese — Interesting surfaces branched over few lines Fabrizio Catanese — Interesting surfaces branched over few lines
Surfaces which are covers of the plane branched over 5 or 6 lines have provided counterexamples to long standing questions, such as Fujita's question on semiampleness of VHS (Dettweiler-Cat); and examples of ball quotients (Hirzebruch), automorphisms acting trivially on integral cohomology (Cat-Gromadtzki), canonical maps with high degree or image-degree (Pardini, Bauer-Cat). I shall survey several new results, and some open questions. Ciro Ciliberto — Genera of curves on a very general surface in Ciro Ciliberto — Genera of curves on a very general surface in 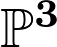
I consider the question of determining the geometric genera of irreducible curves lying on a very general surface 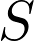 of degree of degree 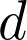 ≥ 5 in ≥ 5 in  (the cases (the cases 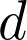 ≤ 4 are well known). First, following a recent joint work with M. Zaidenberg, I indicate an easy proof of non existence of curves of low genera on ≤ 4 are well known). First, following a recent joint work with M. Zaidenberg, I indicate an easy proof of non existence of curves of low genera on 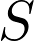 . Then, following another recent joint work with F. Flamini and M. Zaidenberg, I show that the set . Then, following another recent joint work with F. Flamini and M. Zaidenberg, I show that the set 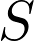 of all non–negative integers which are not realized as geometric genera of irreducible curves on a very general surface of degree in of all non–negative integers which are not realized as geometric genera of irreducible curves on a very general surface of degree in 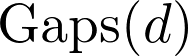 is the union of finitely many disjoint and separated integer intervals. The first of them, according to a theorem of Xu, is is the union of finitely many disjoint and separated integer intervals. The first of them, according to a theorem of Xu, is ![${\rm Gaps}_0(d):=\left[0, \; \frac{d(d-3)}{2} - 3\right]$](rendered/cil5.png) . The next one is . The next one is ![${\rm Gaps}_1(d):=\left[\frac{d^2-3d+4}{2}, \; d^2- 2d - 9\right]$](rendered/cil6.png) for all for all 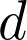 ≥ 6. ≥ 6.
Open questions will be proposed. Igor Dolgachev — Linear systems of quadrics in characteristic two. Igor Dolgachev — Linear systems of quadrics in characteristic two.
The geometry of linear systems of quadrics and the varieties associated with them, like the discriminant variety or the base locus, in characteristic 2 is very different from the case when the characteristic is different from 2. In my talk I will give some examples of this exceptional geometry. In particular, I will explain how to write canonical equations of a quartic del Pezzo surface, or how to treat Reyes congruences and associated with them K3 and Enrique's surfaces in characteristic two. Samuel Grushevsky — Extended period map for cubic threefolds Samuel Grushevsky — Extended period map for cubic threefolds
Taking the intermediate Jacobian of a cubic threefold gives a morphism from the moduli space of smooth cubic threefolds to the moduli space of principally polarized abelian fivefolds. We show that this morphism extends to a morphism from the wonderful compactification of the moduli space of cubic threefolds to the second Voronoi or perfect cone toroidal compactification of A5. This gives a compactified geometric family of intermediate Jacobians over the wonderful compactification, and another approach to degeneration problems for cubic threefolds. Joint work with S. Casalaina-Martin, K. Hulek, and R. Laza Michael Kemeny — Torsion bundles on K3 sections and the Prym-Green conjecture Michael Kemeny — Torsion bundles on K3 sections and the Prym-Green conjecture
Following an approach of Barth and Verra from the late 80s, we construct points in the moduli space 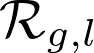 parametrising curves parametrising curves  together with an together with an 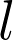 torsion line bundle η for sufficiently high values of the level torsion line bundle η for sufficiently high values of the level 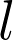 . These points arise as very special sections of certain K3s of Picard rank two. We further verify the Barth-Verra conjecture on the number of such sections. The proof follows by degenerating to specific elliptic K3s of Picard rank 3 where the correct formula appears almost by magic. As a corollary, we deduce the Prym-Green conjecture for odd genus curves and . These points arise as very special sections of certain K3s of Picard rank two. We further verify the Barth-Verra conjecture on the number of such sections. The proof follows by degenerating to specific elliptic K3s of Picard rank 3 where the correct formula appears almost by magic. As a corollary, we deduce the Prym-Green conjecture for odd genus curves and 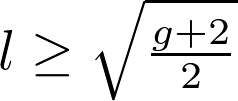 . This is joint work with G. Farkas . This is joint work with G. Farkas Jun Li — Mixed-Spin-P fields and Wall crossing of GW theory of quintics CY Jun Li — Mixed-Spin-P fields and Wall crossing of GW theory of quintics CY
We will introduce the notion of of MSP fields which is a field theory that provides a geometric model for the wall crossing of the GW theory of quintic CY and the FJRW theory of the Fermat quintic, envisioned by Witten. This theory provides a collection of vanishing, which coupled with virtual localization formulas, gives a collection of polynomial relations among the GW and FJRW invariants of quintics. This is a joint work with H.-L. Chang, W.-P. Li and C.-C. Liu. Christian Liedtke — Arithmetic Moduli of Enriques Surfaces Christian Liedtke — Arithmetic Moduli of Enriques Surfaces
Starting from a result of Cossec and Verra over the complex numbers, we show that all Enriques surfaces in arbitrary characteristic arise as quotients of complete intersections of three quadrics in projective 5-space by a finite flat group scheme of order 2. We use this to construct and to describe the local and global geometry of the moduli space of Enriques surfaces in arbitrary characteristic, as well as over the integers. As a byproduct, we show that all Enriques surfaces lift to characteristic zero. Giorgio Ottaviani — Canonical forms of general tensors Giorgio Ottaviani — Canonical forms of general tensors
The Weierstrass form of a pencil of square matrices gives a canonical expression for general tensors of format 2*n*n. In a joint work with Hauenstein, Oeding, Sommese, by using homotopic and numerical techniques, we have found two similar canonical forms in the two formats 3*4*5 and 2*2*2*3. These canonical forms may be explained with an elementary Chern class argument and probably there are no others for general tensors. In the same vein, it may be studied simultaneous Waring decompositions of a vector of homogeneous polynomials. In a few cases, some interesting canonical forms exist, most of them were found one century ago. We expose the complete description obtained by Ciliberto and Russo in the binary case, as well as partial results in the case of more variables. Rahul Pandharipande — Pixton's formula, rational functions, and meromorphic differentials on curves Rahul Pandharipande — Pixton's formula, rational functions, and meromorphic differentials on curves
I will explain a network of new ideas relating a remarkable formula of Pixton, double ramification loci, and the moduli spaces of meromorphic differentials on curves. Gian Pietro Pirola — Fujita decomposition and Massey product Gian Pietro Pirola — Fujita decomposition and Massey product
Motivated by the recent works of Catanese-Dettweiler and of Lu- Zuo we study a secondary operation (Massey product) on the Fujita decomposition of fibered surfaces. We show that the vanishing of the Massey product implies that the monodromy of the unitary part of the Fujita decomposition is finite.
The result is joint work with Sara Torelli. Frank-Olaf Schreyer — Unirational moduli, Hurwitz spaces and random curves Frank-Olaf Schreyer — Unirational moduli, Hurwitz spaces and random curves
In the talk I will report on computer aided unirationality proofs using various models of curves. The goal is to point out the specific difficulty in the constructions for each of the different approaches.  Edoardo Sernesi — A characterization of Brill-Noether-Petri curves lying on a K3 surface Edoardo Sernesi — A characterization of Brill-Noether-Petri curves lying on a K3 surface
A BN-Petri curve of genus g ≥ 23 can be embedded in a polarized K3 surface or in a limit of such if and only if its Wahl map is not surjective. The proof is obtained by establishing two conjectures of J. Wahl. This is joint work with E. Arbarello and A. Bruno. Yuri Tschinkel — Almost abelian anabelian geometry Yuri Tschinkel — Almost abelian anabelian geometry
I will discuss some geometric constructions arising in the study of Galois groups of function fields of algebraic varieties over algebraically closed ground fields (joint with F. Bogomolov). Claire Voisin — Decompositions of the diagonal for cubic hypersurfaces Claire Voisin — Decompositions of the diagonal for cubic hypersurfaces
The existence of a Chow decomposition of the diagonal is an important stable birational invariant which has found recently many applications to the stable version of the Lüroth problem. I will explain several results which are specific to smooth cubic hypersurfaces: for dimension either odd or non greater than 4, having a cohomological and having a Chow-theoretic decomposition of the diagonal are equivalent for them. For a cubic threefold, having a decomposition of the diagonal is equivalent to the minimal class on the intermediate Jacobian being algebraic.Venue
All lectures will take place in the main building of the Humboldt
University at
Karl-Weierstraß-Hörsaal
Room 3038
Unter den Linden 6
10099 Berlin
|

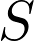 of degree
of degree 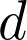 ≥ 5 in
≥ 5 in  (the cases
(the cases 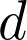 ≤ 4 are well known). First, following a recent joint work with M. Zaidenberg, I indicate an easy proof of non existence of curves of low genera on
≤ 4 are well known). First, following a recent joint work with M. Zaidenberg, I indicate an easy proof of non existence of curves of low genera on 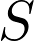 . Then, following another recent joint work with F. Flamini and M. Zaidenberg, I show that the set
. Then, following another recent joint work with F. Flamini and M. Zaidenberg, I show that the set 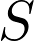 of all non–negative integers which are not realized as geometric genera of irreducible curves on a very general surface of degree in
of all non–negative integers which are not realized as geometric genera of irreducible curves on a very general surface of degree in 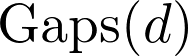 is the union of finitely many disjoint and separated integer intervals. The first of them, according to a theorem of Xu, is
is the union of finitely many disjoint and separated integer intervals. The first of them, according to a theorem of Xu, is ![${\rm Gaps}_0(d):=\left[0, \; \frac{d(d-3)}{2} - 3\right]$](rendered/cil5.png) . The next one is
. The next one is ![${\rm Gaps}_1(d):=\left[\frac{d^2-3d+4}{2}, \; d^2- 2d - 9\right]$](rendered/cil6.png) for all
for all 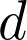 ≥ 6.
≥ 6.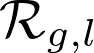 parametrising curves
parametrising curves  together with an
together with an 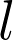 torsion line bundle η for sufficiently high values of the level
torsion line bundle η for sufficiently high values of the level 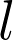 . These points arise as very special sections of certain K3s of Picard rank two. We further verify the Barth-Verra conjecture on the number of such sections. The proof follows by degenerating to specific elliptic K3s of Picard rank 3 where the correct formula appears almost by magic. As a corollary, we deduce the Prym-Green conjecture for odd genus curves and
. These points arise as very special sections of certain K3s of Picard rank two. We further verify the Barth-Verra conjecture on the number of such sections. The proof follows by degenerating to specific elliptic K3s of Picard rank 3 where the correct formula appears almost by magic. As a corollary, we deduce the Prym-Green conjecture for odd genus curves and 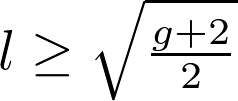 . This is joint work with G. Farkas
. This is joint work with G. Farkas