Introduction
Robust principle component pursuit (RPCP)
aims at decomposing a given data matrix additively into a low-rank
matrix and a sparse matrix. R2PCP
solves such a matrix decomposition problem by formulating the
least-squares problem subject to rank- and cardinality constraints as
follows:
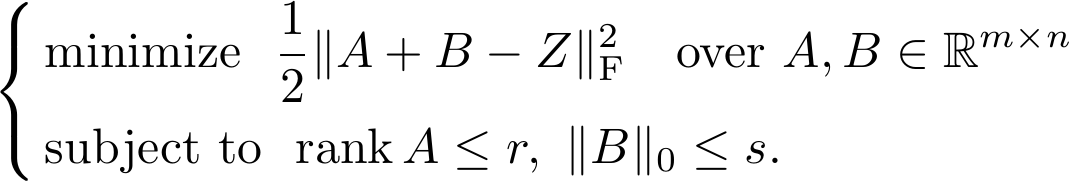
The resulting constrained optimization problem is tackled by an
(inexact) alternating minimization scheme on the respective matrix
manifolds. The sparse matrix subproblem is solved based on sorting. On
the other hand, the low-rank subproblem is resolved by a Riemannian
optimization step on the fixed-rank matrix manifold. Once the Riemannian
gradient and Hessian of the objective are computed, a dogleg descent
path is constructed in the tangent space. This is followed by a
backtracking line search based on a projective retraction. It is proven
theoretically that the overall alternating minimization scheme attains
q-linear convergence under a second-order sufficient condition. Beyond
the (iterative) alternating minimization scheme, we also incorporate,
based on particular applications, a heuristic trimming procedure in
order to adjust r (i.e. the rank of A) and s (i.e. cardinality of B)
dynamically along the iterations.
(Jump to download section)
Demo: Application to surveillance videos
Example 1: Background-foreground separation of video "airport". (a)
original frames; (b) background as low-rank component via R2PCP; (c)
foreground as sparse component via R2PCP; (d) background as low-rank
component via augmented Lagrangian method; (e) foreground as sparse
component via augmented Lagrangian method.









Example 2: Background-foreground separation of video "lobby". (a)
original frames; (b) background as low-rank component via R2PCP; (c)
foreground as sparse component via R2PCP; (d) background as low-rank
component via augmented Lagrangian method; (e) foreground as sparse
component via augmented Lagrangian method.















Downloads
- R2PCP package
- Readme file
- Slide presentation
Please observe the disclaimer information below.
Reference
M. Hintermüller and T. Wu, "Robust Principal Component Pursuit via
Inexact Alternating Minimization on Matrix Manifolds", Journal of
Mathematical Imaging and Vision, to appear.
DOI: 10.1007/s10851-014-0527-y. [link]
[pdf]
Disclaimer
The R2PCP package was developed by Michael Hintermüller from
Department of Mathematics at the Humboldt-University of Berlin and
Tao Wu from Institute for Mathematics and Scientific Computing at
the University of Graz. This work is supported by the Austria
Science Fund (FWF) under START-program Y305 "Interfaces and Free
Boundaries" and the SFB F32 "Mathematical Optimization and
Applications in Biomedical Sciences".
The R2PCP package (including code modifications) may only be used
for NON-COMMERCIAL RESEARCH purposes. For inquiries concerning a
different use, please contact Prof. Michael Hintermüller from the Humboldt-University of Berlin.
Your comments are welcome. Please keep track of bugs or missing/
confusing instructions and report them to
Michael Hintermüller
Tao Wu
The algorithms contained in the R2PCP package were implemented by
Tao Wu.
