![\includegraphics[width=3cm]{huk.eps}](img1.png)
|
HUMBOLDT-UNIVERSITÄT ZU BERLIN
MATHEMATISCH-NATURWISSENSCHAFTLICHE FAKULTÄT II INSTITUT FÜR MATHEMATIK PROF. PHD. ANDREAS GRIEWANK DR. NIEPAGE JAN RIEHME |
![\includegraphics[width=3cm]{huk.eps}](img1.png)
|
Humboldt-Universität zu Berlin,
Institut für Mathematik,
Unter den Linden 6, D-10099 Berlin
Formulieren Sie für das überbestimmte lineare Gleichungssystem
Hinweis: Die ![]() -Norm ist definiert durch
-Norm ist definiert durch
![]() für
für
![]() .
.
Eine Großstadt hat für ein Bauprojekt in den nächsten fünf Jahren jeweils zum Jahresbeginn den folgenden Finanzbedarf:
| Jahr | 1 | 2 | 3 | 4 | 5 | Bemerkung |
| Finanzbedarf | 10 | 8 | 6 | 4 | 2 | in Mio. |
| Aufgenommen im Jahr | 1 | 2 | 3 | 4 | 5 |
| Rückzahlungskurs (in%) | 150 | 140 | 131 | 122 | 114 |
Die Stadtverwaltung steht nun vor der Frage, ob man nicht vielleicht Anleihen auf Vorrat ausgeben soll, also wie die Ausgabemengen der fünf Anleihen zu bemessen sind.1 Die Stadt kann noch nicht benötigte Mittel zu jeweils 7% Verzinsung jährlich (von Jahr zu Jahr) anlegen.
Formulieren Sie ein lineares Optimierungsproblem zur Bestimmung der Ausgabemengen. (15 Punkte)
Zusatzaufgabe: Löse das lineare Optimierungsproblem mittels Standardsoftware ( Matlab, Maple, ...). Interpretiere/Begründe das Ergebnis.(5 Punkte)
Lösen Sie das folgende Problem graphisch und mit dem
Simplex-Algorithmus (per Hand, erste
zulässige Ecke sei
![]() ):
):
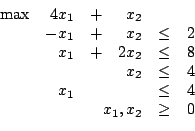 |
Schreiben Sie das LP in allgemeinster Form
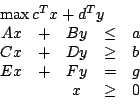 |
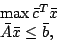 |
Sei
![]() und
und
![]() .
Betrachten Sie das zum primalen Programm (P)
.
Betrachten Sie das zum primalen Programm (P)
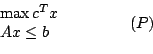 |
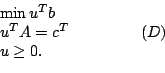 |
Transformieren Sie (D) in die Form
![]() ,
, ![]() . Bilden Sie nun davon das zugehörige duale
Programm (DD). Transformieren Sie (DD) in die Form
. Bilden Sie nun davon das zugehörige duale
Programm (DD). Transformieren Sie (DD) in die Form
![]() ,
, ![]() und vergleichen Sie mit (P).
(15 Punkte)
und vergleichen Sie mit (P).
(15 Punkte)
Betrachtet wird das sogenannte Rucksackproblem:
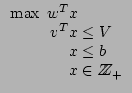
Wenn ![]() das Gesamtvolumen des Rucksacks,
das Gesamtvolumen des Rucksacks, ![]() das
Volumen des
das
Volumen des ![]() -ten Gegenstandes (i=1,...,n) und
-ten Gegenstandes (i=1,...,n) und
![]() dessen Wert sowie
dessen Wert sowie ![]() die zur Verfügung
stehende Anzahl bezeichnet, so besteht das
Rucksackproblem darin, den Rucksack mit einer
Kombination der Gegenstände so zu befüllen, dass
der enthaltene Wert maximal wird ohne das Volumen
die zur Verfügung
stehende Anzahl bezeichnet, so besteht das
Rucksackproblem darin, den Rucksack mit einer
Kombination der Gegenstände so zu befüllen, dass
der enthaltene Wert maximal wird ohne das Volumen ![]() des Rucksacks oder die Vorratsschranken
des Rucksacks oder die Vorratsschranken ![]() der
Gegenstände zu verletzen.
der
Gegenstände zu verletzen.
Löse das Rucksackproblem mit ![]() und
und
| i | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | |
| 4 | 5 | 6 | 7 | |
| 2 | 1 | 2 | 2 |
(25 Punkte)