Prof. Dr. Jürgen Guddat
Wissenschaftlicher Werdegang
| 1960 - 1965 |
Studium der Mathematik an der Humboldt-Universität
zu Berlin |
| 1965 |
Diplom an der Humboldt-Universität zu Berlin |
| 1965 - 1967 |
wissenschaftliche Aspirantur an der Humboldt-Universität
zu Berlin |
| 1967 |
Zusatzstudium an der Universität Bukarest |
| 1968 |
Promotion (Dr. rer. nat.) an der Humboldt-Universität
zu Berlin |
| 1968-71 |
wissenschaftlicher Mitarbeiter an der Humboldt-Universität
zu Berlin |
| 1970 |
Zusatzstudium an der Staatlichen Universität
Leningrad |
| 1971-77 |
Hochschuldozent an der Humboldt-Universität
zu Berlin |
| 1974 |
Promotion B an der Humboldt-Universität
zu Berlin |
| 1977 |
ordentlicher Professor an der Humboldt-Universität
zu Berlin |
| seit 1993 |
Professor (C4) für Mathematik/Optimierung
an der Humboldt-Universität zu Berlin |
|
Wichtigste Forschungsaufenthalte:
| 1974 |
Gastprofessor an der Universität Kairo |
| 1977 |
Gastprofessor an der Karls-Universität Prag |
| 1977-99 |
verschiedene Gastprofessuren an der Universität Havanna |
| 1981, 1985 |
Gastprofessor an der Kepler-Universität Linz |
| 1986,1989 |
Gastprofessor an der Universität Pisa |
Herausgebertätigkeit:
Mitherausgeber der Serie ,,Approximation and Optimization``, Peter
Lang Verlag, Frankfurt a. M., Berlin-Bern-New York-Paris-Wien
Mitarbeit in den Herausgebergremien von Yugoslav Journal of Operations
Research, Journal of Convex Analysis, Revista Investigacion Operacional
Internationale Konferenzserien:
Mitglied der Exekutivkomitees der Konferenzserien ,,Parametric Optimization
and Related Topics`` (V (1997 in Tokio), VI (1999 in Dubrovnik)) und ,,Approximation
and Optimization in the Caribbean`` (IV (1997 in Caracas), V (1999 in Pointe
a Pitre, Guadeloupe), Chairman des Programmkomitees ,,International Conference
on Operations Research`` (im Zweijahresrythmus in Havanna, die 4th im März
2000)
Projekt: Parametrische Optimierung
Beteiligte Wissenschaftler: Dr. W. Gomez, P. Mbunga, Dr. D. Nowack,
C. Solano
Kooperationspartner: Prof. Dra. S. Allende (Universidad de la
Habana), Prof. F. Guerra (Universidad de las Americas, Puebla), Prof. H.
Th. Jongen (RWTH Aachen), Prof. Dr. J.-J. Rückmann (Technische Hochschule
Ilmenau).
Im Mittelpunkt der Untersuchungen stehen einparametrische nichtlineare
Optimierungsprobleme
![\begin{displaymath}P(t): \min \{f(y, t) \vert h_i (y, t) = 0, i \in I, g_j (y, t) \le 0,j \in J\} t \in [0,1]\end{displaymath}](img245.gif)
wobei
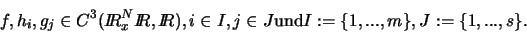
Das Ziel besteht darin, eine Diskretisierung eines vorgegebenen Intervalls ![$[0,1]$](img247.gif) und zugehörige lokale Minimalpunkte, stationäre oder verallgemeinerte
kritische Punkte zu berechnen, wenn ein Startpunkt für
und zugehörige lokale Minimalpunkte, stationäre oder verallgemeinerte
kritische Punkte zu berechnen, wenn ein Startpunkt für 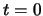 bekannt ist. Kurvenverfolgungstechniken (numerische Verfolgung von Zusammenhangskomponenten
in der Menge
bekannt ist. Kurvenverfolgungstechniken (numerische Verfolgung von Zusammenhangskomponenten
in der Menge 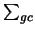 der verallgemeinerten kritischen Punkte erweisen sich als ein wirkungsvolles
Hilfsmittel. Allerdings zeigt sich, daÞ man im allgemeinen mit Kurvenverfolgungsalgorithmen
allein eine solche Diskretisierung nicht berechnen kann. Im ungünstigsten
Fall benötigt man je einen Repräsentanten aus allen Zusammenhangskomponenten.
Deshalb wird versucht, Sprünge (Abstiegsrichtungen) von einer Zusammenhangskomponente
in
der verallgemeinerten kritischen Punkte erweisen sich als ein wirkungsvolles
Hilfsmittel. Allerdings zeigt sich, daÞ man im allgemeinen mit Kurvenverfolgungsalgorithmen
allein eine solche Diskretisierung nicht berechnen kann. Im ungünstigsten
Fall benötigt man je einen Repräsentanten aus allen Zusammenhangskomponenten.
Deshalb wird versucht, Sprünge (Abstiegsrichtungen) von einer Zusammenhangskomponente
in 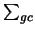 zu einer anderen zu realisieren.
zu einer anderen zu realisieren.
Als theoretisches Fundament spielt die Klasse 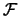 von Jongen-Jonker-Twilt (5 Typen: nicht entarteter kritischer Punkt und
4 Basistypen von Singularitäten ([15], siehe auch [14], [12]) und
die in [14] beschriebenen Sprünge zu anderen Zusammenhangskomponenten
in der Menge
von Jongen-Jonker-Twilt (5 Typen: nicht entarteter kritischer Punkt und
4 Basistypen von Singularitäten ([15], siehe auch [14], [12]) und
die in [14] beschriebenen Sprünge zu anderen Zusammenhangskomponenten
in der Menge 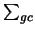 eine entscheidende Rolle. Die wichtigsten Ergebnisse im Berichtszeitraum
werden im folgenden zusammengefasst:
eine entscheidende Rolle. Die wichtigsten Ergebnisse im Berichtszeitraum
werden im folgenden zusammengefasst:
-
(i)
-
Entwicklung einer Klasse von 5 Typen für einparametrische Variationsungleichungen
([8])
-
(ii)
-
Anwendung der für allgemeine einparametrische Optimierungsprobleme
oben kurz dargestellten Theorie und der darauf aufbauenden Lösungsverfahren
(Programmpaket PAFO [3]) zur Lösung nichtlinearer Optimierungsprobleme
([4], [11]) und Vektoroptimierungsprobleme ([5], [10]) sowie lineare Komplementaritätsprobleme
([1]).
Für nichtlineare Optimierungsprobleme wurden die Standard-, Straf-,
exakte Straf- und die Lagrange Multiplikatoreinbettung untersucht. Für
geschickte Modifizierungen der Standard- , Penalty- und Exact Penalty-Einbettung
erhält man mit Hilfe von Kurvenverfolgungsmethoden für einem
beliebigen Startpunkt für 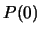 einen stationären Punkt von
einen stationären Punkt von 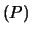 .
Hierbei ist die Zielfunktion
.
Hierbei ist die Zielfunktion 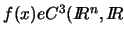 beliebig (also auch nicht notwendig konvex). Für die Restriktionsfunktionen
benötigt man allerdings eine einschränkende Bedingung, die sogenannte
Enlarged Mangasarian Fromovitz-Bedingung (EnMFCQ) ,,Wirklich nichtkonvexe``
Restriktionsfunktionen sind damit ausgeschlossen. Es sei bemerkt, dass
die benutzten Kurvenverfolgungstechniken numerisch stabil sind (siehe [12]
und [14]). Bei dem numerischen Vergleich der drei erfolgreichen Einbettungen
ist der Rechenaufwand bei den ersten beiden Einbettungen geringer. Weiter
sei bemerkt, dass die Originaleinbettungen für die gerechneten Beispiele
nicht erfolgreich waren, was die modifizierten Lagrange Multiplikator-Einbettungen
betrifft, so mussten wir feststellen, dass sie im allgemeinen nicht erfolgreich
sind. Sie sind also ungeeignet für die betrachtete Klasse des Problems
beliebig (also auch nicht notwendig konvex). Für die Restriktionsfunktionen
benötigt man allerdings eine einschränkende Bedingung, die sogenannte
Enlarged Mangasarian Fromovitz-Bedingung (EnMFCQ) ,,Wirklich nichtkonvexe``
Restriktionsfunktionen sind damit ausgeschlossen. Es sei bemerkt, dass
die benutzten Kurvenverfolgungstechniken numerisch stabil sind (siehe [12]
und [14]). Bei dem numerischen Vergleich der drei erfolgreichen Einbettungen
ist der Rechenaufwand bei den ersten beiden Einbettungen geringer. Weiter
sei bemerkt, dass die Originaleinbettungen für die gerechneten Beispiele
nicht erfolgreich waren, was die modifizierten Lagrange Multiplikator-Einbettungen
betrifft, so mussten wir feststellen, dass sie im allgemeinen nicht erfolgreich
sind. Sie sind also ungeeignet für die betrachtete Klasse des Problems 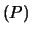 .
Die betrachteten Einbettungen sind spezielle einparametrische Optimierungsprobleme.
Erstmalig wurden topologische Rechtfertigungssätze für die Voraussetzung,
dass die die Einbettungen beschreibenden Funktionen zur Klasse
.
Die betrachteten Einbettungen sind spezielle einparametrische Optimierungsprobleme.
Erstmalig wurden topologische Rechtfertigungssätze für die Voraussetzung,
dass die die Einbettungen beschreibenden Funktionen zur Klasse 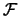 gehören, bewiesen und zwar für die Standardeinbettung ([11] siehe
auch [12]) und für die Strafeinbettung ([8], siehe auch [12]).
gehören, bewiesen und zwar für die Standardeinbettung ([11] siehe
auch [12]) und für die Strafeinbettung ([8], siehe auch [12]).
Auf nichtlineare Vektoroptimierungsprobleme wurde die Standardeinbettung
angewandt ([11]).
In [1] wird eine geschickt modifizierte Penalty-Einbettung auf das
lineare Komplementaritätsproblem (LCP) angewandt. Kurvenverfolgungsmethoden
zur Lösung von (LCP) sind umfangreich untersucht worden. Die in der
Literatur betrachteten Probleme schliessen jedoch Singularitäten aus.
Bei unserem Zugang können Punkte vom Typ 2 und 3 auftreten. Damit
ist die Klasse wesentlich vergrössert worden.
Drittmittel: DFG - Förderung (GU 304/12-1), Förderung
durch das Wissenschaftleraustauschprogramm zwischen der HU und der Universität
Havanna, Förderung durch den DAAD (Kurzzeitdozenturen, Gastaufenthalte
der Kooperationspartner aus Havanna und Puebla, Promotionsstipendien),
Förderung durch das Graduiertenkolleg ,,Geometrie und Nichtlineare
Analysis`` (Promotionsstipendium).
Publikationen
-
[1]
-
Allende, S.; Guddat, J.; Nowack, D.: A modified penalty embedding for linear
complementarity problems. Eingereicht bei: ZOR.
-
[2]
-
Bank, B.; Bustamante, J.; Guddat, J.; Jimenez, M. A.; Jongen, H.Th.; Römisch,
W. (eds.): Proceedings of the 3rd International Conference on Approximation
and Optimization in the Caribbean, Puebla, Mexico, Oktober 8-13, 1995 (Englisch)
Puebla: Benemerita Universidad Autonoma de Puebla, 1997.
-
[3]
-
Dentcheva, D.; Gollmer, R.; Guddat, J.; Rückmann, J.-J.: Pathfollowing
methods in nonlinear optimization II. Exact penalty embedding. In: Florenzano,
M. et al. (eds.), Approximation and Optimization II (Proceedings of the
2nd International Conference on Approximation and Optimization in the Caribbean,
Havana, Cuba, 1993). Ser. Approximation and Optimization, Peter Lang Verlag,
Frankfurt a. M., 1995, 200-230.
-
[4]
-
Gollmer, R.; Kausmann, U.; Mbunga, P.; Nowack, D.; Wendler, K.: Programmpackage
PAFO, 1999.
-
[5]
-
Gomez Bofill, W.; Guddat, J.; Jongen, H. Th.; Rückmann, J.-J.; Solano,
C.: Curvas criticas y saltos en optimizaciÆn no lineal,
web page: http://www.emis.de/monographs/curvas/index.html, submitted
for electronic publication.
-
[6]
-
Gomez Bofill, W.: Vector Optimization: Singularities, Regularizations,
In: Mathematical Methods of Operations Research, ZOR 47 (1998) 3, 473-497.
-
[7]
-
Gomez Bofill, W.: Properties of an interior embedding for solving nonlinear
optimization problems, Mathematical Programming, Series A, 12 (1999), 649-659.
-
[8]
-
Gomez Bofill, W.: On generic quadratic penalty embeddings for nonlinear
optimization problems, Preprint Nr. 97-18, Humboldt-Universität zu
Berlin, Institut für Mathematik, 1997. Erscheint in: Optimization.
-
[9]
-
Gomez Bofill, W.: On a generic class of regular one-parametric variational
inequalities, Preprint Nr. 99-01, Humboldt-Universität zu Berlin,
Institut für Mathematik, 1999. Erscheint in: ZOR.
-
[10]
-
Guddat, J.; Jongen, H. Th.; Nozicka, F.; Still, G.; Twilt, F. (eds.): Parametric
Optimization in Related Topics IV, in Ser. Approximation and Optimization,
Peter Lang Verlag, Frankfurt a. M., 1997.
-
[11]
-
Guddat, J.; Guerra, F.; Nowack, D.: New embeddings for nonlinear multiobjective
optimization problems I, Yugoslav Journal of Operations Research 8 (1988),
45-74.
-
[12]
-
Guddat, J.; Guerra, F.; Nowack, D.: A parametric approach for solution
methods in nonlinear optimization, bookmanuskript.
-
[13]
-
Mbunga, P.: On the double one-parametric optimization problems, Preprint
Nr. 99-8. Weitere Literatur, auf die im Forschungsbericht verwiesen wird:
-
[14]
-
Guddat, J.; Guerra, F.; Jongen, H. Th.: Parametric Optimization: Singularities,
pathfollowing and jumps, B.G. Teubner, Stuttgart; John Wiley & sons,
Chichester 1990.
-
[15]
-
Jongen, H. Th.; Jonker, P.; Twilt, F.: Critical sets in parametric optimization,
Math. Programming 34 (1986), 333-353.


![]() und zugehörige lokale Minimalpunkte, stationäre oder verallgemeinerte
kritische Punkte zu berechnen, wenn ein Startpunkt für
und zugehörige lokale Minimalpunkte, stationäre oder verallgemeinerte
kritische Punkte zu berechnen, wenn ein Startpunkt für ![]() bekannt ist. Kurvenverfolgungstechniken (numerische Verfolgung von Zusammenhangskomponenten
in der Menge
bekannt ist. Kurvenverfolgungstechniken (numerische Verfolgung von Zusammenhangskomponenten
in der Menge ![]() der verallgemeinerten kritischen Punkte erweisen sich als ein wirkungsvolles
Hilfsmittel. Allerdings zeigt sich, daÞ man im allgemeinen mit Kurvenverfolgungsalgorithmen
allein eine solche Diskretisierung nicht berechnen kann. Im ungünstigsten
Fall benötigt man je einen Repräsentanten aus allen Zusammenhangskomponenten.
Deshalb wird versucht, Sprünge (Abstiegsrichtungen) von einer Zusammenhangskomponente
in
der verallgemeinerten kritischen Punkte erweisen sich als ein wirkungsvolles
Hilfsmittel. Allerdings zeigt sich, daÞ man im allgemeinen mit Kurvenverfolgungsalgorithmen
allein eine solche Diskretisierung nicht berechnen kann. Im ungünstigsten
Fall benötigt man je einen Repräsentanten aus allen Zusammenhangskomponenten.
Deshalb wird versucht, Sprünge (Abstiegsrichtungen) von einer Zusammenhangskomponente
in ![]() zu einer anderen zu realisieren.
zu einer anderen zu realisieren.
![]() von Jongen-Jonker-Twilt (5 Typen: nicht entarteter kritischer Punkt und
4 Basistypen von Singularitäten ([15], siehe auch [14], [12]) und
die in [14] beschriebenen Sprünge zu anderen Zusammenhangskomponenten
in der Menge
von Jongen-Jonker-Twilt (5 Typen: nicht entarteter kritischer Punkt und
4 Basistypen von Singularitäten ([15], siehe auch [14], [12]) und
die in [14] beschriebenen Sprünge zu anderen Zusammenhangskomponenten
in der Menge ![]() eine entscheidende Rolle. Die wichtigsten Ergebnisse im Berichtszeitraum
werden im folgenden zusammengefasst:
eine entscheidende Rolle. Die wichtigsten Ergebnisse im Berichtszeitraum
werden im folgenden zusammengefasst: