Discovered misprints in
Differential-Algebraic Equations: A Projector
Based Analysis
|
|
|
|
|
| |
| Page | Line/Place | Misprint | Correction | discovered by |
|
|
|
|
|
| | | | | |
| |
| 27 | (1.44) | u(t) := Πi-1x(t) | u(t) := Πμ-1x(t) | S. Miels |
| 30 | -10 | Gμ = Gμ+ | Gμ = Gμ-1+ | S. Miels |
| 30 | -9 | := I + Qμ-1… | := I + Qμ-1… | S. Miels |
| 30 | -8 | := Qμ-1Gμ-1B0Πμ-2 = | := Qμ-1Gμ-1B
0Πμ-2 = | R. Goodfellow |
| 31 | -7 | QjZj = 0 | QjZj = Qj | S. Miels |
| 31 | -1 | …Y μ-1BΠ
μ-1 | …Y μ-1G
μ-1BΠ
μ-1 | |
| 35 | 2 | (Π3)15 = -α2 | (Π
3)15 = +α2 | |
| 36 | 1 | (P0)11 = 1 | (P0)11 = 0 | |
| 37 | -8,-9 | (Piw + Qiz) | (Piw - Qiz) | |
| 46 | -14 | Xi := K-1X | X
i := K-1X
i | |
| 73 | 10 | B13-(I + B
13-(B
11 +  | B13-(I + (B
11 + 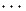 | Ch. Strohm |
| 73 | -6 | 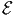 3 := -B13-… 3 := -B13-… | 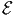 3 := B13-…
3 := B13-… | Ch. Strohm |
| 94 | 16 | DΠμ-1Gμ-1D-u = | DΠ
μ-1Gμ-1B
μD-u = | |
| 96 | Lemma 2.28 (7) | = DΠμ-1Gμ-1BD- | = DΠ
μ-1Gμ-1BΠ
μ-1D- | |
| 145 | -6 | +Γsub(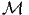 - I)Γsub- - I)Γsub- | +Γsub(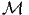 - I)Γsub-- - I)Γsub-- | |
| 146 | in the middle | K = | K-1 = | Vu Hoang Linh |
| 202 | Ex. 3.19 | G1,22 = 2x2 | x2 | Inęs Vilarinho |
| | | Q1,32 = 1∕x2 | x2 | Inęs Vilarinho |
| | | P1,32 = -1∕x2 | -x2 | Inęs Vilarinho |
| | | B1 = B0P0Q1 | B1 = B0P0 | Inęs Vilarinho |
| | | G2,22 = 2x2 + x21 | G
2,22 = x2 + x21 | Inęs Vilarinho |
| 380 | 5 | 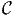 D1( D1(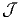 , ℝm) , ℝm) | 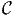 D1(
D1(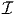 , ℝm) , ℝm) | |
| 491/2 | -3/17 | reference (2.1) | should be (10.12) | |
| 587 | 8 | … ∈ imEB | … ∈ imEA | D. Estévez Schwarz |
| 591 | -3 | Γ := [η1ηr] | Γ := [η1…ηr] | |
| 613 | -5 | = 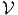 i+1,i+1[1] i+1,i+1[1] | = 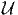 i+1,i+1[1]
i+1,i+1[1] | |
|
|
|
|
|
| |

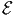 3 := -B13-…
3 := -B13-… 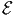 3 := B13-…
3 := B13-… 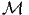 - I)Γsub-
- I)Γsub- 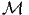 - I)Γsub--
- I)Γsub-- 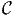 D1(
D1(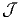 , ℝm)
, ℝm) 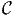 D1(
D1(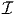 , ℝm)
, ℝm) 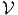 i+1,i+1[1]
i+1,i+1[1] 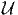 i+1,i+1[1]
i+1,i+1[1]