Solving of IVPs of DAEs by Taylormethods

The integration methods solve initial value problems (IVPs) of DAEs like

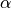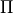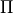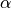with a given initial guess and implicitely defined matrix . The matrix underlines that, in opposit to the ODE case, we can not prescribe initial values for all of the components in the DAE case. The user has to provide the function f and an initial guess only.

The used integration methods are described in [4]: D. Estévez Schwarz and R. Lamour Projected Explicit and Implicit Taylor Series Methods for DAEs Preprint 2019-08, Fachbereich Mathematik, Humboldt-Universität zu Berlin.

Further, the diagnosis of results obtained with other integration methods is also possible.

The integration modules

Three integration modules are offered

Taylor_integration_adaptiveStep(self, t0, T, alpha, max_iterations=20, tol=1e-6, hmin=1e-8, K_start=2, disp=False, RobustIntegration=True, ftol=1e-8, hstart=-1.)

with stepsize control (Attention: The stepsize control works (up to now) on the basis of the explicit Taylormethod (method=0)),

Taylor_integration_timeList(self, ti_list, x0, ftol=1e-14, max_iterations=20)

integrating at given timpoints (e.g. to compare the result with one from another integration method) and,

Taylor_integration_constant_h(self, t0, x0, T, NumSteps, ftol=1e-14, max_iterations=20)

to integrate with constant stepsize.

The diagnosis modules

The diagnosis module

check_solutionpath(self, x, a, b, time_points=100)

computes the index and a condition number along an analytically given function x at constant time_points of the interval [a,b].

The module

check_solution_along_path(self, path, ftol=1e-10)

computes the index and a condition number in given points (e.g. discrete results from another integration method), which are red from a file path.

An example main program

To use the modules you have to prepare your DAE (see How to represent the DAE) and create an instance of the class TaylorIntegration(TaylorDAE) using the constructor

TaylorIntegration(example, K, tol=None, info_output='abc', method=x)

The values for ‘abc’ and x are described in the detailed documentation.

We give here an example to integrate the pendulum problem.

from numpy import array, zeros as npzeros
from IntegrationDAE.DAE_TaylorIntegration import TaylorIntegration

from example_pendulum_u_main import Example_pendulum
ex = Example_pendulum()
n=5
K=10
print ('Solution by minimization')
Taylorex=TaylorIntegration(ex,K,tol=None,info_output='001',method=3)

alpha=array([.5, .5, 0.,0., 0.])
print ('alpha = ',alpha)
t0=0.
T=3.#7.#20.
ftola=1e-12

x0=npzeros(K*n)
x0[:n]=alpha

#NumSteps=100
#yxout,tlist,indexList,condList=Taylorex.Taylor_integration_constant_h(t0,alpha,T,NumSteps,ftol=ftola,max_iterations=300)
yxout,tlist,indexList,condList=Taylorex.Taylor_integration_adaptiveStep(t0,T,alpha,disp=False,tol=1e-7,hstart=1e-6,max_iterations=200)
if yxout is None:
    exit()
print ('indexlist = ',indexList)
print ('condlist = ',condList)
print ('tlist = ',tlist)

Taylorex.plot_figure(tlist,yxout,'x',xlab='t',ylog=False)
Taylorex.plot_figure(tlist,condList,'condition number',xlab='t',ylog=False)
Taylorex.plot_figure(yxout[:,0],yxout[:,1],'phase portrait',xlab='x1',ylog=False)

print ('check_solution_along_path++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++')
path='pendulum_index3_integr_2020-05-12.sol'
print ('path = ',path)
tliste,index,condM=Taylorex.check_solution_along_path(path)
Taylorex.plot_figure(tliste,condM,'condition number from external data',xlab='t',ylog=False)

A detailed main program to use all the different modules can be found at the end of the module DAE_Taylor_integration.