Time and Place
- Tue
| 13:15-14:45 | RUD25 1.114 |
Short Description
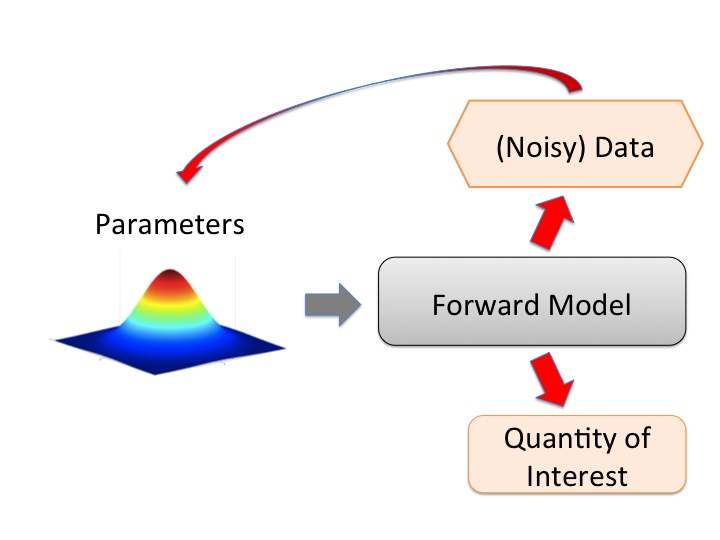
Uncertainty quantification (UQ) is an interesting, fast growing research
area aimed at developing methods to address the impact of parameter,
data and model uncertainty in complex systems. In this seminar, we
will focus on the identification of parameters through observations of
the response of the system - the inverse problem.
The uncertainty in
the solution of the inverse problem will be described via the Bayesian
approach.
We will derive Bayes' theorem in the setting of finite dimensional parameter spaces, and discuss properties such as well-posedness,
statistical estimates and connections to classical regularization methods.
The remainder of this seminar will be
devoted to algorithms for the efficient approximation of the solution of the Bayesian inverse problem.
Literature
J. Kaipio and E. Somersalo, Statistical and Computational Inverse Problems, Springer 2005.
K.J.H. Law, A.M. Stuart and K.C. Zygalakis, Data Assimilation: A Mathematical Introduction. Springer 2015.
S. Reich and C. Cotter, Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge 2015.
Contact
Dr. Claudia Schillings, claudia.schillings[at]hu-berlin.de
Links


