
Application Area: B
Project: B19


 Application Area: B Project: B19 |


|
| Project heads: | Martin Grötschel and Werner Römisch |
| Responsible: | Stefan Vigerske (funded by Matheon) |
| Participants: | Andreas Bley, Ambros Gleixner Thorsten Koch, Marc Pfetsch |
| Duration: | 01.10.2008 - 30.04.2009 |
Mixed-Integer Nonlinear Programming (MINLP) is a hot research topic powered by applications from various areas, including energy generation and distribution, logistics, engineering design, manufacturing, and chemical sciences.
A general MINLP can be formulated as
min f(x)
such that g(x) <= 0
l <= x <= u
xi in Z for all i∈I
where f: Rn → R and g: Rn → Rm
are twice continuously differentiable functions, l, u ∈ Rn determine lower and upper bounds on the
variables, and I ⊆ {1,...,n} denotes the set of variables with
integrality requirements.
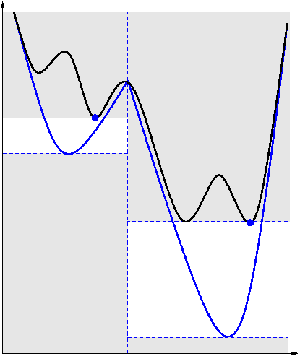 Most state-of-the-art algorithms for finding
globally optimal solutions of general MINLPs are based on branch-and-bound.
Most state-of-the-art algorithms for finding
globally optimal solutions of general MINLPs are based on branch-and-bound.
For MINLPs where the functions f(x) and g(x) are convex, several software packages are available, e.g., SBB, AlphaECP, Bonmin, DICOPT, and FilMINT. Except for SBB and Bonmins B-BB algorithm, these solvers extend an LP-based branch-and-cut solver for mixed-integer linear programming (MILP) by linearizing nonlinear functions whenever appropriate. Thus, their performance highly depends on the underlying MILP solver.
For nonconvex MINLPs, there are numerous application specific approaches.
Only few codes exist, however, that can
handle nonconvex MINLPs in general. The state-of-the-art commercial
MINLP solver BARON implements a spatial branch-and-bound
algorithm that is based on a factorable reformulation of the given problem
and convexifications of univariate functions. The
new open-source code Couenne implements a similar method.
Also the solver LaGO [Now05, NV06] implements a convexification
based branch-and-cut algorithm. Here, nonconvex quadratic terms are
convexified by applying the alpha-underestimating technique from,
while nonconvex nonquadratic functions are first
underestimated by a quadratic function, which is then convexified.
A different methodology called branch-and-infer is pursued in the COCONUT
project. Here, the idea is to embed interval arithmetic and
constraint propagation techniques that reduce bounds on variables and
expressions in a spatial branch-and-bound algorithm.
Currently, COCONUT is able to handle only continuous global optimization
problems, i.e., I is empty.
There also have been efforts to handle nonlinear aspects by combinatorial and integer linear programming techniques. For instance, piecewise linear approximations of nonlinearities proved to be successful in the optimization of gas networks and sheet metal production.
As has been demonstrated by the afore mentioned solvers for convex MINLPs and having recent advantages in mixed-integer linear programming in mind, a favorable way to solve nonconvex MINLPs is the extension of a MILP solver by techniques to handle nonlinear functions (e.g., by convexification and linearization).
|
The goal of this project is to bring together the expertise of SCIP and LaGO for the development of a general purpose LP based branch-and-cut solver for nonconvex MINLPs. Thus, we plan to develop and implement cut generation techniques (e.g., linearizations of convexifications) to cut off infeasible points from an LP relaxation, heuristics (e.g., local search in a nonlinear program (NLP)) to find feasible solution candidates, branching- and node selection rules, and domain propagation methods. In the beginning, we will approach the solution of the broad class of mixed-integer all-quadratic problems (MIQQP), i.e., MINLPs where f(x) and g(x) are quadratic functions. Such constraints appear, for instance, whenever different materials are mixed in technical or chemical processes. Further on, methods for the treatment of other common nonlinear functions and their composition should be developed. An important aspect which had a remarkable impact on MILP solvers but has not found much attention in existing MINLP codes so far is preprocessing. This includes reformulations and model reductions that can be deduced from the problem formulation and that are favorable for the applied algorithm. Therefore, also an adequate in-memory representation of the MINLP demands for special attention. To allow an easy applicability of the developed techniques, interfaces to the modeling systems ZIMPL [Koc04] and GAMS and the instance language OSiL will be developed. In the following, the developed software will be extended step by step to handle more general nonconvex MINLPs.Applications of the developed software are, among others, in fare planning, mine production planing, and the optimization of the design and operation of complex energy conversion systems [AOVNT07, JTV07, JTV09]. Further, the optimization of MINLPs under uncertainties constitutes a challenging application for the developed software. While the deterministic equivalents of stochastic MINLPs are large-scale, their structure offers an interesting starting point for decomposition algorithms [GKNRW02]. |
|
ZIB Project NLIP: Application of the developed software for the solution of open-pit mine production scheduling problems.
ZIB Project VPP: Application of the developed software for the solution of vehicle positioning problems.
TU Darmstadt, Research Group Optimization: Development of an NLP infrastructure in SCIP and interface to the NLP solver DONLP.
TU Braunschweig, Institute for Mathematical Optimization: Development of SCIP to support implementation of MINLP plugins.
GAMS Development: Development of a GAMS interface to an extended SCIP version.
| [Ach07] | T. Achterberg. Constraint Integer Programming. Dissertation, Technische Universität Berlin, 2007. ZIB-Report 08-01. |
| [AOVNT07] | T. Ahadi-Oskui, S. Vigerske, I. Nowak, and G. Tsatsaronis. Optimizing the design of complex energy conversion systems by branch and cut. Preprint 07-11, Department of Mathematics, Humboldt-University Berlin, 2007. |
| [GKNRW02] | N. Gröwe-Kuska, K.C. Kiwiel, M.P. Nowak, W. Römisch, and I. Wegner. Power management in a hydro-thermal system under uncertainty by Lagrangian relaxation. In C. Greengard and A. Ruszczynski, editors, Decision Making Under Uncertainty - Energy and Power, pages 39-70. Springer, 2002. |
| [JTV07] | M. Jüdes, G. Tsatsaronis, and S. Vigerske. Entwurfsoptimierung von Energieumwandlungsanlagen mit mehreren Betriebspunkten. In Optimierung in der Energiewirtschaft, VDI-Berichte 2018, pages 199-210. VDI-Verlag, Düsseldorf, 2007. |
| [JTV09] | M. Jüdes, G. Tsatsaronis, and S. Vigerske. Optimization of the design and partial-load operation of power plants using mixed-integer nonlinear programming. In: Optimization in the Energy Industry (J. Kallrath, P. Pardalos, S. Rebennack, M. Scheidt eds.), Springer, 2009. |
| [Koc04] | T. Koch. Rapid Mathematical Programming. Dissertation, Technische Universität Berlin, 2004. ZIB-Report 04-58. |
| [Now05] | I. Nowak. Relaxation and Decomposition Methods for Mixed Integer Nonlinear Programming. Birkhäuser Verlag, Basel, Schweiz, 2005. |
| [NV06] | I. Nowak and S. Vigerske. LaGO - a (heuristic) branch and cut algorithm for nonconvex MINLPs. Central European Journal of Operations Research 16:2, 127-138 (2008) |