Fehlerkorrekturen zu dem Buch "Didaktik der
Analytischen Geometrie und Linearen Algebra" von H.-W. Henn
und A. Filler
Errata
Auf dieser Seite werden nach der Drucklegung bekannt
gewordene Fehler berichtigt.
Fehler in dem Kapitel 1
- Bislang sind keine Fehler in dem Kapitel 1 des Buches bekannt.
Fehler in dem Kapitel 2
Fehler in dem
Kapitel 3
- In der Definition 3.2 auf S. 94 wurde der
Fall vergessen, dass Anfangs- und Endpunkte bei beiden gerichteten
Strecken jeweils identisch sind (es sich also um "Nullpfeile" handelt.
Dies führt dazu, dass die Nullpfeilklasse (später als
Nullvektor bezeichnet) in der Definition auf S. 95 nicht erfasst
wird. Daher ist die Definition 3.2 folgendermaßen zu
ergänzen:

- In
der Definition 3.3 auf S. 95 wird die
Bezeichnung
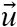 sowohl für Pfeile als auch für
Pfeilklassen verwendet. Auch wenn dies vorher erwähnt wird, kann
es zu Missverständnissen führen, siehe hierzu die Anmerkungen von Prof. Dr.
Hermann Hähl (Universität Stuttgart).
sowohl für Pfeile als auch für
Pfeilklassen verwendet. Auch wenn dies vorher erwähnt wird, kann
es zu Missverständnissen führen, siehe hierzu die Anmerkungen von Prof. Dr.
Hermann Hähl (Universität Stuttgart). - Die Frage,
warum das Koordinatentupel, das
man einem Pfeil zuordnet, nur von dessen Pfeilklasse
abhängt (Abschnitt 3.3.4, S. 113ff.), wird nur recht
oberflächlich diskutiert. Vielen Dank
an Prof. Dr. Hermann Hähl (Universität Stuttgart)
für eine exakte
Erörterung dieser Frage.
Fehler in dem
Kapitel 4
- Im Abschnitt 4.3, S. 183 heißt es in Bezug auf die
Ebenengleichung ax + by + cz = d:
"Ist ein Koeffizient, etwa c, gleich null, so gibt es je einen
Schnittpunkt A mit der x-Achse und B mit der y-Achse."
Korrektur: Die Existenz eines Schnittpunkts etwa mit der
x-Achse hängt
nicht von c ab, sondern vielmehr von a: Ist a ungleich null, so
existiert genau ein Schnittpunkt; ist a = 0, so existiert kein
Schnittpunkt, falls d ungleich 0; ist schließlich a = 0 = d, so
liegt
die ganze x-Achse in der Ebene. - Im Abschnitt 4.5.4 steht auf S.
215 (unter "Abstand Punkt-Gerade"):
"Aus der Dreiecksungleichung folgt, dass die kürzeste Entfernung
eines
Punkts P von einer Geraden g sich durch das Lot ergibt."
Die Begründung ist nicht korrekt. Eine richtige Begründung
ist mithilfe der Beziehung "größere Seite -
größerer Winkel" im Dreieck oder mithilfe des Satzes des
Pythagoras möglich.
Fehler in dem Kapitel 5
- Bislang sind
keine Fehler in dem Kapitel 5 des Buches bekannt.
Fehler in dem Kapitel 6
- Bislang sind keine Fehler in
dem Kapitel 6 des Buches bekannt.
Fehler in dem
Kapitel 7
- Bislang sind keine Fehler in dem Kapitel 7
des Buches bekannt.
